Calibration Defined

Calibration refers to the process of verification that a measuring instrument is within its designated accuracy. This is usually accomplished by formal comparison with a standard which is traceable to national standards (NIST in the USA) and certified reference materials. (source: wikipedia)

How RI does it?
The RI calibration process compiles a deviation chart of phase and magnitude so that the measurements reported can be correlated to the actual value being measured. The measurement errors created by the various components in the system are accounted for and removed from the actual value that is reported for the measurement.

Roos Instruments ATE systems use a complex number with both phase and magnitude that allows greater accuracy than magnitude calibration alone because we can use mathematical error correction to recreate the actual values as they appear at the device. By calculating the exact lengths of wire along the measurement path, we can measure the affect the DUT has on the system to determine the measurement.

Background
Physical dimensions is measured by the system. We can rely on mathematical models to remove the impact of the components used in the measurement of the device.

Real Numbers vs Imaginary Numbers
Imaginary numbers are encountered when measuring a frequency and magnitude because both elements create a circle rotating around a two dimensional chart, whereas a magnitude only measurements can be charted on a number line. (more info: see Wikipedia)

This can best be illustrated in the following example: Measure 3 voltages = A, B, and C

Magnitude values on a number line:
     A    B    C
|----*----*----*----->

Same measurements with complex numbers:

    |
    | *A
    |       C
|---|-------*--------->
    |
    |    *B
(diagram is missing magnitude arrows at all the same lengths)

As you can see, the voltage measurements were at different frequencies and actually represent the same magnitude (distance from origin).

Geometric interpretation

Geometrically, imaginary numbers are found on the vertical axis of the complex number plane, allowing them to be presented orthogonal to the real axis. One way of viewing imaginary numbers is to consider a standard number line, positively increasing in magnitude to the right, and negatively increasing in magnitude to the left. At 0 on this x-axis, a y-axis can be drawn with "positive" direction going up; "positive" imaginary numbers then "increase" in magnitude upwards, and "negative" imaginary numbers "decrease" in magnitude downwards. This vertical axis is often called the "imaginary axis" and is denoted as simply Im.

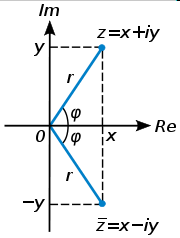
In this representation, multiplication by −1 corresponds to a rotation of 180 degrees about the origin. Multiplication by i corresponds to a 90-degree rotation in the "positive" direction (i.e. counter-clockwise), and the equation i² = − 1 is interpreted as saying that if we apply 2 90-degree rotations about the origin, the net result is a single 180-degree rotation. Note that a 90-degree rotation in the "negative" direction (i.e. clockwise) also satisfies this interpretation. This reflects the fact that −i also solves the equation x² = − 1 — see imaginary unit.

In mathematics, the complex numbers are an extension of the real numbers obtained by adjoining an imaginary unit, denoted i, which satisfies:^[1]

Every complex number can be written in the form a + bi, where a and b are real numbers called the real part and the imaginary part of the complex number, respectively.

Complex numbers are a field, and thus have addition, subtraction, multiplication, and division operations. These operations extend the corresponding operations on real numbers, although with a number of additional elegant and useful properties, e.g., negative real numbers can be obtained by squaring complex (imaginary) numbers.

Signal analysis

Complex numbers are used in signal analysis and other fields for a convenient description for periodically varying signals. For given real functions representing actual physical quantities, often in terms of sines and cosines, corresponding complex functions are considered of which the real parts are the original quantities. For a sine wave of a given frequency, the absolute value |z| of the corresponding z is the amplitude and the argument arg(z) the phase.

If Fourier analysis is employed to write a given real-valued signal as a sum of periodic functions, these periodic functions are often written as complex valued functions of the form

where ω represents the angular frequency and the complex number z encodes the phase and amplitude as explained above.

In electrical engineering, the Fourier transform is used to analyze varying voltages and currents. The treatment of resistors, capacitors, and inductors can then be unified by introducing imaginary, frequency-dependent resistances for the latter two and combining all three in a single complex number called the impedance. (Electrical engineers and some physicists use the letter j for the imaginary unit since i is typically reserved for varying currents and may come into conflict with i.) This approach is called phasor calculus. This use is also extended into digital signal processing and digital image processing, which utilize digital versions of Fourier analysis (and Wavelet analysis) to transmit, compress, restore, and otherwise process digital audio signals, still images, and video signals.

Thermal expansion of Copper and why we use ovens?

source: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thexp.html

0.00017 m
for copper ( 17 per degree C x10^-6)
from 25 deg C to 35 deg C

Example: Put a 5V Sine wave at 6 Ghz across a 100 cm copper wire. As the temperature changes, so to does the length and resistance of the wire. The wave length is 5 cm. The temperature change of copper is




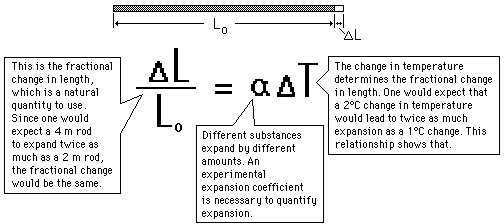
Material Fractional expansion of Copper is 17 per degree C x10^-6

What it does?

Removes the errors created by the system